The following proof was discovered by Tom M. Apostol, and was published as “Irrationality of the Square Root of Two – A Geometric Proof” in the American Mathematical Monthly, November 2000, pp. 841–842.
In short, if \(\sqrt{2}\) were rational, we could construct an isosceles right triangle with integer sides. Given one such triangle, it is possible to construct another that is smaller. Repeating the construction, we could construct arbitrarily small integer triangles. But this is impossible since there is a lower limit on how small a triangle can be and still have integer sides. Therefore no such triangle could exist in the first place, and \(\sqrt{2}\) is irrational.
In oher words, suppose that \(\sqrt{2}\) is rational. Then by scaling up the isosceles right triangle with sides 1, 1, and \(\sqrt{2}\) appropriately, we obtain the smallest possible isosceles right triangle whose sides are all integers.
Note: If \(\sqrt{2}=a/b\), where \(a/b\) is in lowest terms, then the desired tringle has catheti with length b and hypotenuse a. Indeed, for the pythagorean theorem, we have:
\(b^2+b^2=a^2 \Leftrightarrow 2b^2=a^2\)
but, for hypothesis, \(a=\sqrt{2}b\). So: \(2b^2=2b^2\).
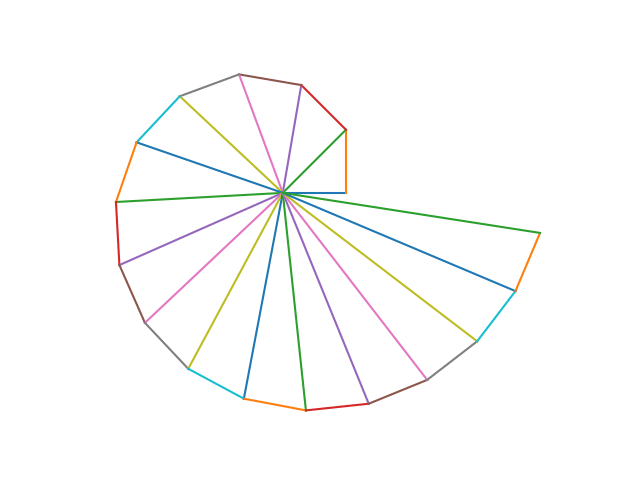
This is \(\Delta OAB\) in the figure below:
By hypothesis, OA, OB, and AB are all integers.
Now construct arc BC, whose center is at A.
Note: \(AC=AB\), and thus AC is an integer. Since \(OC = OA – CA\), OC is also an integer.
Let CD be the perpendicular to OA at point C. Then \(\Delta OCD\) is also an isosceles right triangle, so OC = CD, and CD is an integer.
\(\overline {CD}\) and \(\overline {BD}\) are tangents to the same arc from the same point D, so \(CD = BD\), and BD is an integer. Since OB and BD are both integers, so is OD.
Since OC, CD, and OD are all integers, \(\Delta OCD\) is another isosceles right triangle with integer sides, which contradicts the assumption that \(\Delta OAB\) was the smallest such.
The logical contradiction we have arrived at shows that \(\sqrt{2}\) is a irrational number.